2.4 Confronto tra espansione dello spazio e curvatura dello spazio-tempo
Riepilogando quanto
esposto nei paragrafi precedenti:
- lo spazio è una sostanza nella quale si manifestano sia la materia che le
onde elettromagnetiche, ha una espansione che è influenzata dalla presenza della
materia ed è più espanso vicino alle masse materiali e sempre meno espanso man mano
che ci si allontana da esse;
- gli oggetti materiali tendono a muoversi verso dove lo spazio è più espanso e
quindi verso altri oggetti materiali;
- la velocità della luce è isotropa solo rispetto allo spazio;
- la velocità alla quale scorre il tempo, è funzione dell'espansione dello spazio,
e cioè più lo spazio è espanso e più rallenta il tempo;
- dato che lo spazio è sempre meno espanso, man mano che ci si allontana dalla
superficie della Terra, il tempo scorre più velocemente man mano che ci si
allontana dalla Terra, come risulta dalle osservazioni (per esempio, nel GPS).
In conclusione lo spazio è euclideo ed ha tre dimensioni ed un grado di
espansione, e la velocità alla quale scorre il tempo è funzione del grado di
espansione dello spazio nel
luogo dove viene misurato.
Ora provo a spiegare perchè, invece, per la Relatività Generale (RG) lo
spazio-tempo è curvo.
In base ai risultati dell'esperimento di Michelson e Morley (MM), dai quali
risulta che la velocità della luce è isotropa rispetto a qualunque sistema di
riferimento inerziale (ma secondo Lorentz tale risultato è viziato dal
rallentamento del tempo e dalla contrazione dell'interferomentro di MM, in
funzione della sua velocità rispetto allo spazio - che per Lorentz corrisponde
all'etere), Einstein ha dedotto la teoria della Relatività Ristretta (RR), le
cui trasformazioni usano le tre dimensioni spaziali più la dimensione temporale,
per cui lo spazio è "diventato" spazio-tempo.
Successivamente Einstein, con la RG, ha dimostrato che la velocità del tempo è
funzione della gravità e, quindi, della distanza al quadrato dalle masse
materiali, come poi risultò anche dalle osservazioni.
Infatti nel paragrafo 6.6 del capitolo relativo alla RG, del suo libro “Sei
pezzi meno facili” (8), Feynman dimostra lo scostamento tra due orologi
situati a quote diverse.

Feynman trova anche
il valore numerico dello scostamento per 20 metri di dislivello, e cioè circa 2
x 10**(-15), e cioè di circa 1 x 10**(-16) per metro di dislivello.
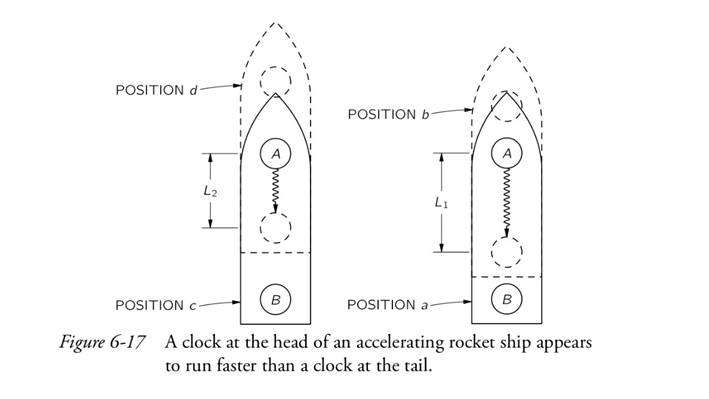
Lo dimostra ragionando su un'astronave accelerata (Fig. 6-17), in cui si capisce che se si
mandano due segnali da prua a poppa distanziati di un secondo, essi arrivano
distanziati di meno di un secondo. Quindi per un osservatore accanto
all’orologio a poppa, quello a prua va più veloce.
Dopo di che pone l'astronave sulla superficie terrestre ed usa il Principio di
Equivalenza (PE) per dedurre che l'effetto che si vedeva nell'astronave
accelerata si deve vedere anche nel campo gravitazionale terrestre.
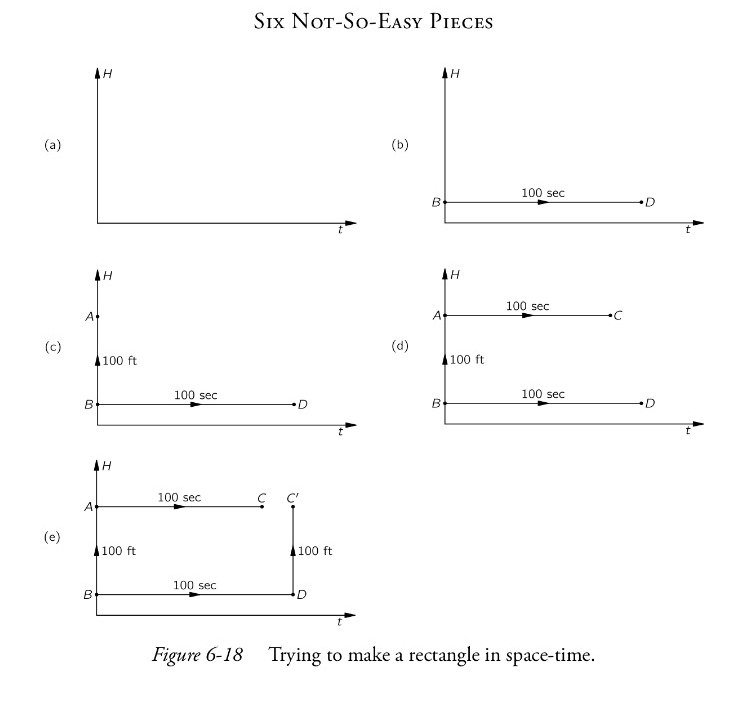
Poi nel paragrafo 6.7, basandosi sui ragionamenti esposti nel paragrafo 6.6,
Feynman dimostra la curvatura dello spazio-tempo aiutandosi coi disegni di cui
figura 6-18 sotto riportata.
Ecco come lo
dimostra.
“Cerchiamo di fare un po’ di geometria dello spazio-tempo. Questo alla prima può
sembrare strano, però abbiamo spesso costruito diagrammi dello spazio-tempo con
la distanza riportata su un asse ed il tempo su un altro. Supponiamo di cercar
di costruire un rettangolo nello spazio-tempo. Cominciamo col tracciare un
grafico dell’altezza H in funzione di t come in Fig. 6-18 (a). Per aver la base
del rettangolo prendiamo un oggetto che è fermo all’altezza H₁ e seguiamo la sua
linea d’universo per 100 secondi. Otteniamo la linea BD nella parte (b) della
figura, che è parallela all’asse t. Ora prendiamo un altro oggetto che si
trova 100 piedi sopra al primo al tempo t = 0. In partenza ci si trova al punto
A della Fig. 6-18 (c). Ora seguiamone la linea d’universo per 100 secondi,
misurati con l’orologio in A. L’oggetto va da A in C come si vede nella parte
(d) della figura. Ma si noti che siccome il tempo va a ritmo diverso alle due
altezze – si ammette che ci sia un campo gravitazionale – i due punti C e D non
sono simultanei. Se si cerca di completare il rettangolo tracciando una retta
fino al punto C che si trova 100 piedi sopra D, allo stesso tempo – come in Fig.
6-18 (e) – i pezzi non si raccordano. E questo è ciò che si intende quando si
dice che lo spazio-tempo è curvo.”
In altre parole,
mentre per le ipotesi qui presentate, il fatto che i segmenti alle altezze A e
B, abbiano una lunghezza diversa, dipende dal fatto che il grado di espansione dello
spazio a dette altezze è diversa, per la RG detto fatto dimostra che lo
spazio-tempo è curvo.
In conclusione, secondo le presenti ipotesi, lo spazio è euclideo e possiede un
grado di espansione, e la velocità del tempo è funzione di detto grado di
espansione.
Mentre per la RR lo spazio è "diventato" spazio-tempo, che per la RG è curvo.
In pratica, quindi, sia per le ipotesi qui presentate che per la RG, si tratta dello stesso fenomeno, anche se visto da punti di vista diversi (tolemaico per la RG e copernicano per le ipotesi qui presentate), pertanto tutto quanto previsto dalla RG, dovrebbero valere anche per le ipotesi qui presentate.