HOME PAGE -

IPOTESI BASATE SULLA TEORIA SUL MOTO RELATIVO ALLO SPAZIO IN ESPANSIONE
 

RIASSUNTO 

Nella teoria sul moto relativo allo spazio in espansione (1), ho affermato che da essa si possono derivare ulteriori ipotesi sui vari fenomeni dell'Universo, più compatibili con le osservazioni.
Ed ora, con questo articolo, mi propongo di esporre tali ipotesi, che spiegano vari fenomeni dell’Universo in una modalità compatibile con detta teoria e più aderente con le osservazioni rispetto a quella attualmente sostenuta dalla Comunità Scientifica.

Ecco, in breve, le ipotesi.

L’Universo è composto esclusivamente da un’infinità di quanti di spazio che tendono ad espandersi, causando anche la propria espansione.
La materia si manifesta su insiemi di quanti di spazio, che vengono mediamente compressi, consentendo ai quanti vicini e poi via via a quelli più lontani, di espandersi di più.
La gravità è dovuta al fatto che ogni oggetto tende a muoversi verso i quanti di spazio meno compressi e, quindi, verso altri oggetti, con le leggi relative alla Relatività Generale. Presento anche una modifica alla formula della gravità universale, per renderla compatibile con questo modello di Universo.
La velocità della luce dipende dalla compressione dei quanti di spazio dei luoghi nei quali essa transita, nel senso che maggiore è la loro compressione, maggiore è la sua velocità. Ma poiché anche gli orologi si muovono più o meno velocemente, in funzione di detta compressione, la velocità della luce risulta sempre la stessa in qualunque luogo. Pertanto, nel passato, quando la compressione dei quanti di spazio era maggiore, anche la velocità della luce era maggiore.
Il redshift cosmologico è dovuto alla velocità del luogo dove si sta muovendo l’oggetto celeste che riceve il fotone, rispetto al luogo dove si stava muovendo l’oggetto celeste che l’ha emesso, in un Universo la cui espansione sta decelerando. A sostegno di queste ipotesi presento due tabelle che simulano il viaggio dei fotoni di una galassia ad alto redshift e quello dei fotoni della Radiazione Cosmica di Fondo, ed anche una formula per ottenere la luminosità apparente compatibile con le osservazioni delle supernove Ia ad alto redshift. Inoltre dimostro che considerando il redshift cosmologico come dovuto all’espansione dello spazio, come attualmente sostiene la Comunità Scientifica, non si può giustificare la luminosità apparente degli oggetti celesti con elevato redshift.

1. INTRODUZIONE

Nella teoria sul moto relativo allo spazio in espansione (1) ho affermato che da essa si possono derivare ulteriori ipotesi sui vari fenomeni dell'Universo, più compatibili con le osservazioni.
Ed ora, con questo articolo, mi propongo di esporre tali ipotesi, che spiegano vari fenomeni dell’Universo, quali la sua espansione, la gravità, la velocità della luce, il redshift cosmologico,  in una modalità compatibile con detta teoria e più aderente con le osservazioni rispetto a quella attualmente sostenuta dalla Comunità Scientifica (CS).

Premetto che se in molti casi userò il presente anziché il condizionale, non lo farò per esprimere certezze, ma solo per semplicità di esposizione.

2. UNIVERSO DI QUANTI DI SPAZIO

2.1 Universo in espansione

L’Universo si può immaginare come un’immensa sfera composta esclusivamente da un’infinità di piccolissime particelle indivisibili di una uguale quantità di spazio, che d’ora in poi denominerò come "quanti di spazio".

Per spazio intendo una sostanza continua, quindi non composta di particelle (che significa che le piccolissime particelle non sono a loro volta composte di ulteriori ancora più piccole particelle), che tende ad espandersi. In pratica si tratta dell’unica vera sostanza che compone l’Universo e che, pertanto, deve essere molto diversa dalla materia che noi possiamo osservare.

Durante il cosiddetto Big Bang, i quanti erano estremamente compressi e quindi hanno iniziato ad espandersi, causando l’espansione dell’Universo, che sta continuando tutt’ora.

La velocità di espansione dell’Universo è la stessa in tutti i luoghi dell’Universo, per cui ogni luogo si allontana da ogni altro luogo con una velocità che dipende dalla distanza: più sono lontani e più velocemente si allontanano tra di loro.
Quindi ogni luogo può considerarsi come un centro dell’Universo, dal quale tutti gli altri luoghi si allontanano.

2.2 Gravità

Tra i quanti di spazio non esiste alcun vuoto, per cui se un quanto si comprime, e quindi riduce le proprie dimensioni, i quanti adiacenti possono/devono aumentare le loro dimensioni e, quindi, espandersi.

La materia è composta da quanti di spazio.

Le particelle elementari del cosiddetto modello standard della fisica quantistica, sono dei fenomeni fisici che, tra l’altro, comprimono quanti di spazio e, pertanto, un oggetto materiale contiene moltissimi insiemi di quanti di spazio compressi, che fanno aumentare la compressione media dei quanti di spazio che lo compongono.
Così i quanti limitrofi all’oggetto, e cioè quelli in prima linea, grazie alla riduzione delle dimensioni dei quanti dell’oggetto, possono/devono espandersi di più. Ma poi vengono ricompressi parzialmente perché i quanti in seconda linea, che sono più compressi per non aver ancora “subito” espansioni, si espandono a loro volta verso quelli di prima linea. Poi anche i quanti di terza linea, ancora compressi, si espandono verso quelli di seconda linea. E così via fino ai quanti sempre più lontani dall’oggetto.
In parole povere la materia, comprimendo numerosi quanti di spazio, consente ai quanti vicini e poi via via anche a quelli sempre più lontani, di potersi espandere di più.
Il risultato è un ambiente nel quale i quanti di spazio vicini alla materia sono più espansi di quelli via via più lontani dalla materia.
I quanti che compongono la materia, sono comunque più compressi rispetto ai quanti esterni ad essa però, per precisione, bisogna dire che è la compressione media dei quanti che compongono la materia, che è maggiore della compressione media dei quanti esterni alla materia. Perché all’interno degli atomi vi sono molti quanti che potrebbero essere anche più espansi di quelli esterni alla materia, e cioè, per esempio, quelli tra i nuclei e gli elettroni, in quanto più vicini alle particelle elementari.

Gli insiemi di quanti che compongono gli atomi, tendono ad espandersi in direzione dei quanti più espansi (o meno compressi), perché trovano meno resistenza alla propria espansione. Pertanto anche gli oggetti materiali, dato che sono composti da atomi, si espandono in direzione dei quanti più espansi, e quindi in direzione di altri oggetti. Per questo motivo ogni oggetto tende a muoversi verso altri oggetti.
Per muovere un oggetto in direzione contraria a quella nella quale tenderebbe a muoversi, e cioè da un punto dove i quanti sono più espansi (per esempio dal livello terra) ad un punto dove sono meno espansi (per esempio ad un metro da terra), si deve usare una certa energia (che viene persa da chi muove l’oggetto), con la quale gradualmente viene aumentata la compressione degli insiemi di quanti (che così aumentano la loro energia interna) che compongono gli atomi dell’oggetto, in modo tale che riescano ad opporsi alla maggiore pressione dei quanti che trovano man mano che si avvicinano al livello più alto. Però, più precisamente, non bisogna pensare a dei quanti che si muovono da un punto ad un altro, ma a delle compressioni di quanti che si muovono da un punto ad un altro o, meglio ancora, a delle manifestazioni fisiche che avvengono nei vari punti dello spazio.
Di conseguenza un oggetto di un metro di altezza, ha gli atomi situati più in alto con una compressione media maggiore rispetto agli atomi situati più in basso, in quanto i quanti che compongono gli atomi situati più in alto trovano più resistenza alla loro espansione rispetto ai quanti che compongono gli atomi situati più in basso. Quindi ponendo che l’oggetto abbia la forma di un cubo, avrà la superficie inferiore più estesa di quella superiore, in quanto la compressione dei quanti vicini alla superficie inferiore è minore di quella dei quanti vicini alla superficie superiore. Ma se misurate, le due superficie risulterebbero uguali, in quanto anche gli atomi degli strumenti di misura sono influenzati dall’espansione dei quanti vicini.

Ora vorrei fare delle considerazioni sulla formula della gravitazione universale di Newton e proporre delle modifiche, perché essa non risulta compatibile col presente modello di Universo, in quanto esso prevede due cause per l’espansione dei quanti di spazio:
- quella dovuta alla presenza della materia, per la quale i quanti di spazio si espandono senza contribuire ad espandere l’Universo (perché la loro espansione viene bilanciata dalla compressione dei quanti che costituiscono la materia);
- quella dovuta all’espansione nativa dei quanti di spazio, per la quale i quanti di spazio si espandono facendo espandere anche l’Universo.
Per cui è necessario modificare la formula della gravità universale di Newton, per tenerne conto.

La formula attuale della gravità universale è la seguente:

Dalla quale ricavo quella dell’accelerazione di gravità per un oggetto di piccola massa, e cioè:

dove:
- g è l’accelerazione di gravità;
- G è una costante gravitazionale universale;
- M è la massa di un ipotetico oggetto celeste;
- d  è la distanza dell’oggetto di piccola massa.

Ma questa formula riguarda solo l’accelerazione relativa all’espansione dei quanti dovuta alla presenza della materia, pertanto non comprende quella relativa all’espansione nativa dei quanti di spazio, che va in direzione contraria e, quindi, si oppone all’accelerazione dovuta alla gravità.

Per cui la formula dell’accelerazione di gravità completa, in base al mio modello di Universo, è la seguente:

dove E è una costante di accelerazione dovuta all’espansione dello spazio, che è la stessa per tutto l’Universo e che si riduce nel tempo in funzione della decelerazione dell'espansione dell'Universo, e che va valorizzata in base alle osservazioni.
Ma per far tornare i conti bisogna aumentare il valore della costante gravitazionale, in quanto il valore g da ricavare, è dovuto anche al valore della costante di accelerazione. 

Quindi bisogna valorizzare le due costanti della formula, in modo che i suoi risultati siano compatibili con le osservazioni, le quali dimostrano che nelle lunghe distanze il valore di g non è perfettamente inversamente proporzionale al quadrato della distanza. Come nel caso degli oggetti celesti più esterni alle galassie.
Inoltre dalla formula risulta che una volta superata una determinata distanza, il valore relativo all’accelerazione dovuta all’espansione dello spazio, supera il valore dovuto alla gravitazione, per cui risulta che l’oggetto di piccola massa si allontana dall’oggetto celeste. Come risulta dalle osservazioni.
Pertanto valorizzando adeguatamente le costanti della formula, non potrebbe essere possibile giustificare determinati moti degli oggetti celesti, anche senza la necessità di ipotizzare l’esistenza della materia e dell’energia, oscure?

2.3 Velocità e frequenza dei fotoni, variabili

E' stato rilevato sperimentalmente che
(1) la gravità influenza lo scorrere del tempo e la frequenza ondulatoria dei fotoni e quindi anche la loro lunghezza d'onda.
Ma, per la presente ipotesi,
(2) la gravità è dovuta all’espansione dello spazio.
Di conseguenza si può affermare che
(3) l’espansione dello spazio influenza lo scorrere del tempo (più lo spazio è espanso e più gli orologi rallentano) e la frequenza ondulatoria dei fotoni e quindi anche la loro lunghezza d'onda.
Ma poiché risulta anche che
(4) la velocità della luce è sempre la stessa in qualunque luogo la si misuri e, quindi, per qualunque velocità dello scorrere del tempo,
ne consegue che
(5) anche la velocità della luce si adegua all’espansione dello spazio e cioè che la luce va più o meno velocemente in funzione della più o meno elevata espansione dello spazio.
Quindi nel passato,
(6) quando lo spazio dell’Universo era molto meno espanso, la luce aveva una velocità molto superiore a quella attuale, anche se ipotetici orologi di allora l'avrebbero misurata sempre a 300.000 km/s (perché avrebbero misurato il tempo più velocemente, perché lo spazio era meno espanso).
In altre parole, man mano che l’Universo si è espanso, la luce ha ridotto la sua velocità, ma anche ipotetici orologi avrebbero rallentato, facendo così misurare la velocità della luce sempre a 300.000 km/s.

Come ho dimostrato nel punto 3, l’espansione dello spazio influenza la frequenza ondulatoria dei fotoni. Più precisamente fa rallentare la loro frequenza ondulatoria, ma senza che ipotetici orologi possano rilevarlo, in quanto l’espansione fa rallentare anch’essi della stessa misura. Perché se così non fosse, la frequenza dei fotoni emessi da una determinata tipologia di fonte (per esempio dall’idrogeno) e misurata con uno stesso orologio, risulterebbe maggiore in cima ad una montagna (dove lo spazio è meno espanso), rispetto alla sua base (dove lo spazio è più espanso).
Quindi nel passato, quando lo spazio era meno espanso, la frequenza dei fotoni emessi da una determinata tipologia di fonte (per esempio dall’idrogeno), era molto maggiore rispetto ad ora, per poi rallentare man mano che l’Universo si è espanso. Ma ipotetici orologi non avrebbero rilevato alcun rallentamento della frequenza, in quanto anch’essi avrebbero rallentato della stessa misura.
In pratica è come se quei fotoni fossero essi stessi un orologio.

2.4 Confronto espansione dello spazio e curvatura dello spazio-tempo

Riepilogando quanto sopra esposto:
-  lo spazio è una sostanza nella quale si manifestano sia la materia che le onde elettromagnetiche;
- ha una densità che è influenzata dalla presenza della materia.
- è meno denso vicino alle masse materiali e sempre più denso man mano che ci si allontana da esse;
- gli oggetti materiali tendono a muoversi verso dove lo spazio è meno denso e cioè verso altri oggetti materiali;
- la velocità della luce è isotropa solo rispetto ad esso;
- la velocità con la quale scorre il tempo, è funzione della densità dello spazio e cioè più lo spazio è denso e più veloce scorre il tempo.
- dato che lo spazio è sempre più denso, man mano che ci si allontana dalla superficie della Terra, il tempo scorre più velocemente man mano che ci si allontana dalla Terra, come risulta nella realtà (per esempio, nel GPS).
In conclusione, secondo le presenti ipotesi, lo spazio è euclideo ed ha tre dimensioni ed una densità, e la velocità del tempo è funzione della densità dello spazio nel luogo dove viene misurato.

Ora provo a spiegare perchè, invece, per la Relatività Generale (RG) lo spazio-tempo è curvo.
In base ai risultati dell'esperimento di Michelson e Morley (MM), dai quali risulta che la velocità della luce è isotropa rispetto a qualunque sistema di riferimento inerziale (ma secondo Lorentz tale risultato è viziato dal rallentamento del tempo e dalla contrazione dell'interferomentro di MM, in funzione della sua velocità rispetto allo spazio - che per Lorentz corrisponde all'etere), Einstein ha dedotto la teoria della Relatività Ristretta (RR), le cui trasformazioni usano le tre dimensioni spaziali più la dimensione temporale, per cui lo spazio è "diventato" spazio-tempo.
Successivamente Einstein, con la RG, ha dimostrato che la velocità del tempo è funzione della distanza dalle masse materiali, come poi risultò anche nella realtà (per esempio, nel GPS).
Infatti nel paragrafo 6.6 del capitolo relativo alla RG, del suo libro “Sei pezzi meno facili” (8), Feynman dimostra lo scostamento tra due orologi situati a quote diverse.

Feynman trova anche il valore numerico dello scostamento per 20 metri di dislivello, e cioè 2x10**(-15), e cioè di 1x10**(-16) per metro di dislivello.
Lo dimostra ragionando su un'astronave accelerata, in cui si capisce che se si mandano due segnali da prua a poppa distanziati di un secondo, essi arrivano distanziati di meno di un secondo. Quindi per un osservatore accanto all’orologio a poppa, quello a prua va più veloce.
Dopo di che pone l'astronave sulla superficie terrestre ed usa il Principio di Equivalenza (PE) per dedurre che l'effetto che si vedeva nell'astronave accelerata si deve vedere anche nel campo gravitazionale terrestre.
Poi nel paragrafo 6.7 basandosi sui ragionamenti esposti nel paragrafo 6.6, Feynman dimostra la curvatura dello spazio-tempo aiutandosi coi grafici di cui figura 6.18.

Ecco come lo dimostra.
"Cerchiamo di fare un po’ di geometria dello spazio-tempo. Questo alla prima può sembrare strano, però abbiamo spesso costruito diagrammi dello spazio-tempo con la distanza riportata su un asse ed il tempo su un altro. Supponiamo di cercar di costruire un rettangolo nello spazio-tempo. Cominciamo col tracciare un grafico dell’altezza H in funzione di t come in Fig. 6-18 (a). Per aver la base del rettangolo prendiamo un oggetto che è fermo all’altezza H1 e seguiamo la sua linea d’universo per 100 secondi. Otteniamo la linea BD nella parte (b) della figura, che è parallela all’asse t. Ora prendiamo un altro oggetto che si trova 100 piedi sopra al primo al tempo t = 0. In partenza ci si trova al punto A della Fig. 6-18 (c). Ora seguiamone la linea d’universo per 100 secondi, misurati con l’orologio in A. L’oggetto va da A in C come si vede nella parte (d) della figura. Ma si noti che siccome il tempo va a ritmo diverso alle due altezze – si ammette che ci sia un campo gravitazionale – i due punti C e D non sono simultanei. Se si cerca di completare il rettangolo tracciando una retta fino al punto C che si trova 100 piedi sopra D, allo stesso tempo – come in Fig. 6-18 (e) – i pezzi non si raccordano. E questo è ciò che si intende quando si dice che lo spazio-tempo è curvo.”

In altre parole, mentre per le ipotesi qui presentate, il fatto che i segmenti delle altezze A e B, abbiano una lunghezza diversa, dipende dal fenomeno che la densità dello spazio in dette altezze è diversa, per la RG detto fatto dimostra che lo spazio-tempo è curvo.
In conclusione, secondo le presenti ipotesi, lo spazio è euclideo e possiede una densità, e la velocità del tempo è funzione di detta densità.
Mentre per la RR lo spazio è "diventato" spazio-tempo, che per la RG è curvo.

In pratica, quindi, sia per la presente ipotesi che per la RG, si tratta dello stesso fenomeno, anche se visto da punti di vista diversi, pertanto tutto quanto previsto dalla RG, dovrebbero valere anche per il modello di Universo qui presentato.

3. MODELLO DI UNIVERSO

Il rallentamento della frequenza ondulatoria dei fotoni ed il conseguente allungamento della loro lunghezza d'onda, dovuta all’espansione dello spazio, viene denominata dalla Comunità Scientifica (CS) come “redshift cosmologico”.
Però nel paragrafo 2.3 ho sostenuto che assieme a detto rallentamento di frequenza, avviene anche un rallentamento degli orologi della stessa misura.
In conclusione, quindi, l'espansione dello spazio non fa misurare, almeno direttamente, alcuna riduzione della frequenza ondulatoria dei fotoni e, quindi, neanche il redshift cosmologico.
E allora a cosa sarebbe dovuto l’elevato valore del redshift rilevato nei fotoni provenienti dagli oggetti celesti molto lontani?
Come dimostrerò qui di seguito, è dovuto alla velocità di allontanamento del luogo dove si sta muovendo l’oggetto celeste che riceve il fotone, rispetto al luogo dove si stava muovendo l’oggetto celeste che l’ha emesso.
Quindi tale redshift è comunque dovuto all’espansione dello spazio, in quanto è l’espansione che fa allungare le distanze tra i luoghi dell’Universo e, quindi, fa aumentare le velocità di allontanamento dei luoghi dell’Universo.

A sostegno di queste ipotesi presento due tabelle:
- la prima, che simula il viaggio dei fotoni di una galassia ad alto redshift, anche utilizzando la luminosità apparente degli oggetti celesti ad alto redshift;
- la seconda, che simula il viaggio della Radiazione Cosmica di Fondo (abbreviata in CMBR, dall'inglese Cosmic Microwave Background Radiation).

3.1 Esemplificazione del modello di Universo

Per far meglio comprendere le due simulazioni sopracitate, le faccio precedere da una semplice esemplificazione.

Si immagini l’Universo in espansione come una grande sfera di gomma che si stia gonfiando continuamente e sulla cui superficie siano segnati moltissimi punti (raffigurano luoghi dello spazio).
Si immagini poi una galassia come un camioncino che si muova sulla superficie della sfera ad una velocità di 0,1 m/s, ma restando sempre vicino ad uno dei punti.
Poi si immagini la Terra come un altro camioncino, che si muova anch’esso nei pressi di un punto ad una velocità di 0,1 m/s.
A causa dell’espansione della sfera, i due punti citati si allontanano l’uno dall’altro ad una determinata velocità e, di conseguenza, anche i due camioncini si allontanano l’uno dall’altro alla stessa velocità (per precisione, più o meno qualcosa in funzione della direzione del loro moto).

Si immaginino poi i fotoni come un insieme di automobiline che si muovano sulla superficie della sfera a velocità costante, poniamo di 1 m/s.
Si osserverà che a causa della dilatazione della superficie della sfera, i punti si allontanano l'uno dall'altro, per cui ogni automobilina avrà una velocità di 1 m/s rispetto al punto sopra il quale sta transitando, ma una velocità diversa rispetto agli altri punti segnati sulla superficie della sfera.
Se un'automobilina parte dal punto del camioncino raffigurante la galassia, e va verso il punto del camioncino raffigurante la Terra, alla partenza ha una velocità di 1 m/s rispetto al punto di partenza, ma inferiore rispetto a quello di arrivo, in quanto quest'ultimo si sta allontanando a causa della dilatazione della superficie della sfera.
Ma durante il viaggio aumenta sempre di più la sua velocità rispetto al punto di partenza, a causa del continuo aumento della distanza tra il punto sul quale essa sta transitando (sempre ad 1 m/s) ed il punto di partenza. Infine arriva alla velocità di 1 m/s rispetto al punto di arrivo, il quale ha una determinata velocità rispetto al punto di partenza. Pertanto l’automobilina avrà una velocità superiore ad 1 m/s, di detta determinata velocità, rispetto al punto di partenza.

3.2 Simulazione del viaggio dei fotoni di una galassia ad alto redshift

Come ho scritto sopra, lo spazio si sta espandendo alla stessa velocità in tutti i luoghi dell’Universo. Pertanto ogni luogo si sta allontanando da ogni altro luogo, con una velocità che dipende dalla distanza.
In pratica ogni luogo può considerarsi come al centro dell’Universo, in quanto tutti gli altri luoghi si allontanano da esso, ma anche perché i fotoni che lo percorrono, vi hanno la stessa velocità, e cioè 300.000 km/s, in tutte le direzioni.
Ma se i fotoni hanno una velocità di 300.000 km/s rispetto al luogo che stanno percorrendo, ed i luoghi che via via percorrono si allontanano sempre più velocemente dal luogo della loro emissione, ne consegue che anche i fotoni aumentano sempre più la loro velocità rispetto al luogo di emissione.
Per esempio i fotoni emessi da una galassia e diretti verso la Terra, nel momento dell'emissione hanno una velocità di 300.000 km/s rispetto al luogo della galassia (per precisione dovrei scrivere “luogo dove si sta muovendo”, perché ogni oggetto celeste non è a riposo rispetto a detto luogo, ma per brevità scrivo solo ”luogo”), ma molto inferiore rispetto al luogo della Terra (più precisamente dovrei scrivere “luogo dove si starà muovendo la Terra nel momento dell’arrivo”, ma per brevità qui scrivo solo “luogo della Terra”), perché esso si sta allontanando dal luogo della galassia.
Ma man mano che i fotoni procedono verso il luogo della Terra, percorrendo luoghi che si allontanano sempre più velocemente dal luogo della galassia, i fotoni aumentano sempre di più la loro velocità rispetto al luogo della Terra, fino ad arrivarci alla velocità di 300.000 km/s rispetto ad esso.
Tale aumento di velocità corrisponde alla velocità del luogo ricevente rispetto a quello emittente, e viene usato come fattore per calcolare il cosiddetto redshift cosmologico, che si indica con il simbolo "z" . Il cui valore incrementato di 1, corrisponde al rapporto tra la velocità della luce e la differenza tra la stessa e la velocità del luogo ricevente rispetto a quello di emissione (formula 3.2.1)

Dove “vr” sta per velocità del luogo del ricevente.

Questa è una formula dell'effetto Doppler, che considera il ricevente in moto e la sorgente ferma, dalla quale si può ottenere quella per la velocità del luogo ricevente e cioè (formula 3.2.2):

Invece la formula usata dalla CS, considera il ricevente fermo e la sorgente in moto, per cui il fattore z risulta dalla divisione tra la velocità della sorgente e quella della luce. Di conseguenza per trovare la velocità della sorgente conoscendo il fattore z, si deve moltiplicarlo per la velocità della luce (formula 3.2.3)

velocità sorgente = z x c

Ma per la CS il fattore z si riferisce all’espansione dello spazio e non ad una velocità di allontanamento tra i vari luoghi dello spazio.
Per precisione faccio rilevare che oltre che dal redshift cosmologico, il fattore z è composto anche dai redshift dovuti ai moti degli oggetti emittente e ricevente, rispetto ai rispettivi luoghi, che se i valori del redshift sono elevati, risultano poco rilevanti.

Per esempio un redshift di 0,59 misurato sulla Terra, indica che la Terra si sta allontanando dalla galassia, di 111.321 km/s.

Per far meglio comprendere come funziona il tutto in base al mio modello di Universo, tramite l’applicazione excel ho sviluppato una tabella di simulazione del viaggio verso la Terra, dei fotoni di una galassia ad alto redshift, che espongo qui di seguito.
Ho sviluppato la tabella al solo scopo di dimostrare la sostenibilità della presente ipotesi per cui, pur avendo cercato di ottenere risultati aderenti alla realtà, posso presentarli solo a titolo di esempio.
Per quanto riguarda i valori relativi al redshift, mi sono basato su quelli che ho trovato in un articolo dell’astronomo Vincenzo Zappalà (2).

Espongo qui di seguito le modalità che ho seguito per calcolare i valori esposti in tabella, ma in generale, perché un’esposizione precisa sarebbe troppo lunga, (però potrei inviare la tabella in formato excel, a chi me lo chiedesse).

Premetto che rispetto al foglio di lavoro excel, dal quale è stata ricavata la tabella, per mancanza di spazio orizzontale ho dovuto nascondere due colonne: la prima, che sarebbe stata contrassegnata dalla lettera B, che contiene la velocità dei fotoni rispetto ai luoghi percorsi, e cioè sempre 300.000 km/s in ogni casella; la seconda, che sarebbe stata contrassegnata dalla lettera G, che contiene la distanza percorsa dai fotoni rispetto ai luoghi, e cioè sempre 1 miliardo di anni luce in ogni casella.

Prima di tutto, per ogni periodo, in base al redshift ho calcolato la velocità media con la quale i luoghi dello spazio via via percorsi dai fotoni, si stanno allontanano dal luogo della galassia, usando formule ricavate dalla 3.2.2, e l’ho inserita nelle caselle della colonna “velocità  luogo di transito” (contrassegnata dalla lettera C).
Poi ho sommato tale velocità a quella della luce rispetto ai luoghi percorsi (300.000 km/s), inserendo il risultato nelle caselle della colonna “velocità  fotoni + luogo” (D).
Indi ho calcolato la distanza percorsa dai fotoni, dividendo i valori esposti nella colonna “velocità  fotoni + luogo” (D) per 300.000, ed ho inserito i valori progressivi nelle casella della colonna “distanza  fotoni + luogo” (H).
Poi ho ottenuto ed inserito i suoi valori progressivi nelle caselle della colonna “distanza progressiva  fotoni + luogo” (L).
Come si può osservare, nell’ultima casella risulta il valore di 8,536 miliardi di anni luce, che corrisponde alla somma della distanza totale percorsa dai fotoni con la distanza di allontanamento dei luoghi percorsi, somma che corrisponde alla distanza attuale tra il luogo della galassia e quello della Terra.
Poi tramite una formula sulla luminosità apparente (3.3.1), la cui spiegazione si può trovare nel paragrafo 3.3 (per spiegare meglio la formula, avevo bisogno della tabella, quindi ho dovuto posporre la spiegazione), ho ricavato il rapporto tra la distanza attuale e quella del momento dell’emissione dei fotoni, rapporto che corrisponde al fattore di espansione dello spazio durante il viaggio dei fotoni, ed poi ho calcolato la distanza al momento dell’emissione dei fotoni, che risulta di 5,040 miliardi di anni luce.
Poi, grazie alle funzioni di excel, ho variato dicotomicamente la velocità della Terra alla partenza, fino a quando nell’ultima casella della colonna “distanza progressiva – diff.za” (K) è stato ottenuto il valore 0 (Terra raggiunta), e così per ogni periodo ho ottenuto la velocità media di allontanamento del luogo della Terra da quello della galassia, che ho calcolato in funzione dei redshift dei vari periodi e che ho inserito nelle caselle della colonna “velocità  luogo Terra” (F).
Infine, per ogni periodo ho calcolato anche la distanza di allontanamento del luogo della Terra rispetto a quello della galassia, e ho inserito il suo valore della colonna “distanza  luogo Terra” (I), mentre ho inserito il suo valore progressivo nelle caselle della colonna “distanza progressiva  luogo Terra” (M).

Dalla tabella si può rilevare che all’inizio del viaggio il luogo della Terra si trova a 5,040 miliardi di anni luce di distanza da quello della galassia, luogo che a causa dell’espansione dello spazio tra esso stesso e quello della galassia, si sta allontanando alla velocità di 275.000 km/s dal luogo della galassia, facendo così allontanare anche la Terra nei confronti della galassia.
Nei periodi successivi risulta che la velocità con la quale il luogo della Terra si allontana da quello della galassia, diminuisce, di conseguenza risulta che l’espansione dello spazio, decelera (questo fenomeno verrà ripreso anche nel paragrafo 3.4).
Infine quando i fotoni arrivano alla Terra, il luogo della Terra si trova a 8,536 miliardi di anni luce da quello della galassia, e la sua velocità di allontanamento da quello della galassia, risulta di 111.321 km/s.

Durante il loro viaggio, sempre a causa dell’espansione dello spazio, anche i fotoni variano di velocità rispetto al luogo della galassia, ma in aumento, perché transitano in luoghi sempre più lontani da quello della galassia e che, quindi, si allontanano sempre più velocemente dalla galassia.
Infine i fotoni arrivano al luogo della Terra, alla velocità di 300.000 km/s rispetto ad esso, ma di 411.321 km/s rispetto al luogo della galassia.

3.3 Formula per il calcolo della luminosità apparente degli oggetti celesti ad alto redshift

Qui di seguito, utilizzando come esempio i dati della tabella esposta nel paragrafo precedente, presento una formula che credo più compatibile con le osservazioni di quella sostenuta dalla CS, per ottenere l’espansione dello spazio avvenuta durante il viaggio dei fotoni di un oggetto celeste ad alto redshift, utilizzando la sua luminosità apparente. Cosa che ritengo importante anche per dimostrare che l’espansione dell’Universo sta decelerando, anziché accelerando come sostenuto dalla CS, basandosi proprio sulla luminosità apparente degli oggetti celesti ad alto redshift, come le supernove di tipo Ia.
Infatti ecco cosa ha scritto il fisico Matteo Billi nella sua tesi di laurea (3):
“Le SNe Ia vengono utilizzate in cosmologia come indicatori di distanza. Nel 1998 due team di ricerca, il Supernova Cosmology Project e l’High-z Supernova Search Team compirono degli studi su un campione di SNe in galassie lontane a z = 0.2 ÷ 0.9. Da questi lavori emerse che le luminosità apparenti erano tipicamente inferiori del 25% rispetto ai valori attesi. Questo indica che tali oggetti si trovano ad una distanza di luminosità superiore a quella prevista da modelli d’Universo dominati da materia. Venne quindi determinata per la prima volta l’evidenza di un Universo in condizione di espansione accelerata.”.

Per la formula qui presentata, i fattori per i quali dividere la luminosità assoluta (L) per ottenere quella apparente (l), sono i seguenti.

1. Area della superficie della sfera con raggio corrispondente alla distanza percorsa dai fotoni (F) rispetto ai luoghi via via attraversati (per problemi di spazio tale distanza non è stata esposta in tabella, ma corrisponde alla velocità della luce, per il numero degli anni, e cioè a 7 miliardi di anni luce). Perché mano a mano che si muovono, i fotoni si distribuiscono in una superficie di sfera sempre più ampia, in quanto il suo raggio si allunga. Ma va considerata solo la distanza percorsa dai fotoni rispetto ai luoghi via via attraversati, e non anche la distanza alla quale si sono allontanati i luoghi attraversati rispetto al luogo della galassia, a causa dell’espansione dello spazio, in quanto questo allontanamento viene considerato nel secondo fattore.

2. Rapporto tra la distanza attuale (d1) e la distanza iniziale (d2) al cubo. Questo rapporto corrisponde all’espansione dello spazio avvenuta durante il viaggio (E), che è uniforme in tutti i luoghi dell’Universo e, quindi, anche in quelli dove sono transitati i fotoni della galassia (sono rispettivamente l’ultimo ed il primo valore, della colonna “distanza  progressiva  luogo Terra” (M)). Il valore dell’espansione va elevato al cubo, in quanto si tratta di un’espansione volumetrica, che quindi avviene sulle tre dimensioni spaziali.

Quindi la formula è la seguente:

e sostituendo il fattore E con i fattori relativi alle distanze attuale e iniziale, si ha la seguente formula (formula 3.3.1):

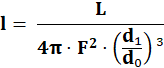
Mentre la formula usata dalla CS, che ho trovato in rete (4), è la seguente (formula 3.3.2):

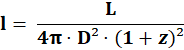
Dove "D" rappresenta la distanza attuale tra l’emittente ed il ricevente.
Per quanto riguarda il fattore (1 + z), in base a quanto ho trovato in rete, va elevato al quadrato per i seguenti motivi:
“- un fattore è necessario per tenere conto del fatto che ogni fotone perde energia a causa del redshift;
- un secondo fattore è dovuto al fatto che anche il ritmo di arrivo dei fotoni è inferiore al ritmo di emissione ancora per lo stesso fattore”.
Quindi la formula della CS considera come raggio della sfera la distanza attuale e non la distanza effettivamente percorsa dai fotoni (quindi senza quella dovuta all’espansione), come giustificato nella spiegazione della mia formula.
Inoltre il fattore di espansione sostenuto dalla CS, viene elevato al quadrato anziché al cubo.
Per cui rispetto alla mia formula, si ha il fattore D che ha un valore maggiore del fattore F ed il fattore che esprime l’espansione dello spazio (1 + z) al quadrato, che dovrebbe corrispondere ad un valore minore rispetto al fattore E al cubo.
Queste differenze dovrebbero essere dovute ad interpretazioni diverse sulle cause della riduzione di luminosità che avviene durante il viaggio dei fotoni.

Preciso che i valori relativi al redshift cosmologico (0,59) ed alla distanza attuale tra emittente e ricevente (8,68), li ho ricavati dall’articolo di Zappalà (2) già citato, e sono relativi ai fotoni emessi 7 miliardi di anni fa da un oggetto celeste. Ho scelto il redshift di 0,59 (e quindi i fotoni emessi 7 miliardi di anni fa da una galassia), in quanto è il più vicino alla media tra i redshift minimo e massimo citati nella tesi di Matteo Billi (3), e cioè (0,2 ÷ 0,9), per cui dovrebbe valere anche il 25% di luminosità in meno citato nella tesi, che dovrebbe corrispondere ad una media di riduzioni di luminosità.

Per ottenere l’espansione dello spazio avvenuta durante il viaggio dei fotoni, mi basta usare solo alcuni fattori di ciascuna delle due formule, in quanto gli altri fattori sono uguali. 

Faccio rilevare che utilizzando solo parte del denominatore e la distanza in miliardi di anni luce, non ricavo il valore reale della luminosità apparente, ma un indice di luminosità apparente, che posso utilizzare per fare dei rapporti tra risultati relativi a luminosità apparenti e che per lo scopo di questo articolo, ritengo sia sufficiente.

Per quanto riguarda la formula della CS, i fattori sono quelli contenuti nell’espressione D²·(1 + z)²,dalla quale risulta:

8,68² x (1 + 0,59)² = 75,3424 x 2,5281 = 190,473

Poiché in base a quanto riportato nella tesi di laurea di Billi (3), dalle osservazioni risulta che la luminosità apparente osservata è del 25% inferiore a quella calcolata (naturalmente in base alla formula della CS), trovo il valore dell’indice di luminosità apparente, incrementando quest’ultima del 25%.

190,473 x 1,25% = 238,108

Questo valore mi serve per calcolare il rapporto tra la distanza attuale e la distanza alla partenza dei fotoni, tra la Terra ed il luogo di partenza dei fotoni e, quindi, il fattore di espansione dello spazio durante il viaggio dei fotoni.

Nella corrispondente espressione usata dalla mia formula, e cioè    , valorizzo i dati conosciuti ed ottengo:

Poi divido per 49 (7 x 7) i due membri ed estraggo la radice cubica del membro a destra:

Che costituisce il rapporto di espansione dello spazio durante il viaggio dei fotoni della galassia.

Infine, con l’ultimo passaggio

d0 = 5,040

ottengo la distanza tra il luogo della Terra e quello della galassia emittente, all’inizio del viaggio.
Poi inserisco questa distanza nella tabella e potrò così completare la simulazione del viaggio dei fotoni della galassia, con la modalità esposta nel paragrafo precedente.

Per maggior chiarezza riassumo le modalità di calcolo.
Prima utilizzo i redshift dei vari periodi, per simulare il viaggio dei fotoni fino al loro arrivo sulla Terra, ottenendo la distanza percorsa dai fotoni comprensiva di quella dovuta all’espansione dello spazio che, in pratica, corrisponde alla distanza attuale tra la galassia e la Terra.
Poi applicando la formula 3.3.1, utilizzo la luminosità apparente osservata per trovare la distanza tra la galassia e la Terra, alla partenza dei fotoni.
Ed infine completo la simulazione modificando dicotomicamente la velocità con la quale al Terra si stava allontanando dalla galassia, alla partenza dei fotoni.
In breve uso i redshift per trovare la distanza attuale e poi uso la luminosità apparente per trovare l’espansione dello spazio.

Alcune considerazioni sui risultati della simulazione e sulla mia formula.

Faccio rilevare che c’è una lieve differenza tra la distanza attuale usata dalla formula della CS, che è di 8,68 miliardi di anni luce ed è stata ricavata dall’articolo di Zappalà (2), e quella usata dalla mia formula, che è di 8,536 ed è stata ricavata dallo sviluppo della simulazione qui presentata. Ciò è dovuto al fatto che io ho considerato i redshift cosmologici come fattori per il calcolo delle velocità di recessione di ciascun periodo, per ottenere la distanza attuale.
Infatti dei dati di Zappalà, considero soltanto i redshift di ogni periodo, che utilizzo per calcolare la velocità dei luoghi nei quali stanno transitando i fotoni, rispetto al luogo dove sono stati emessi.
Per quanto riguarda la distanza iniziale, la differenza è maggiore in quanto l’articolo di Zappalà la indica in 5,46 miliardi di anni luce, mentre per la mia simulazione risulta di 5,04. Ciò è dovuto al fatto che io ho considerato un’espansione dello spazio maggiore, per giustificare la minore luminosità apparente osservata delle supernove di tipo Ia.
Volendo considerare valida la distanza di 8,68 miliardi di anni luce, anziché quella ottenuta dalla simulazione, applicando la mia formula sulla luminosità apparente, si ottiene una distanza iniziale di 5,12, che comunque è vicina ai 5,04 della mia simulazione.

Però i cosmologi che volessero valutare le distanze in base al mio modello di Universo, dovrebbero ottenere delle distanze minori di quelle esposte nell’articolo di Zappalà (perché dovrebbero considerare una maggior espansione dello spazio e quindi una maggiore riduzione della luminosità apparente in funzione della distanza) e, quindi, potrebbero anche risultare inferiori a quelle ottenute dalla simulazione. Che comunque non sono molto precise, perché considerano una velocità media di recessione, per ciascun miliardo di anni.
In conclusione, volendo basarsi sul modello di Universo qui considerato, i risultati delle osservazioni andrebbero rivalutati, pur sapendo, in ogni caso, che si tratta di valutazioni che possono solo avvicinare alla realtà.

3.4 Simulazione del viaggio dei fotoni della radiazione di fondo

In base alla teoria del Big Bang, circa 380.000 anni dopo l’inizio della sua espansione, l’Universo è diventato trasparente alla radiazione, per cui un’enorme quantità di fotoni ha iniziato a propagarsi liberamente (5, 6).
I fotoni sono partiti da luoghi diversi dell'Universo ed hanno viaggiato in direzioni casuali, per cui una parte di essi ha viaggiato in direzione del luogo della Terra.
Da allora tali fotoni, che vengono denominati come CMBR, hanno continuato ad arrivare sulla Terra, a cominciare da quelli partiti dai luoghi più vicini e poi via via, da quelli sempre più lontani.
Durante il viaggio i fotoni si trovano a percorrere luoghi che a causa dell’espansione dello spazio, si allontanano sempre più velocemente dai luoghi di partenza, per cui anch’essi aumentano la loro velocità rispetto ai luoghi di partenza, fino ad arrivare al luogo della Terra, alla velocità di 300.000 km/s rispetto ad esso, ma molto superiore rispetto ai luoghi della loro partenza.
Ed aumentando la velocità aumenta anche il redshift.
Durante il tempo trascorso da allora, lo spazio ha continuato ad espandersi e, di conseguenza, è aumentata la velocità di allontanamento del luogo della Terra da quello di partenza dei fotoni della CMBR.
Così anche il redshift è andato via via aumentando, fino ad arrivare ai valori attuali, di circa 1.100.
Quindi, attualmente, applicando la formula 3.2.2, esposta nel paragrafo 3.2, la velocità del luogo della Terra rispetto ai luoghi di partenza dei fotoni della CMBR, risulta di circa 299.728 km/s.

Utilizzando questo redshift ed anche quelli dei vari periodi, e con modalità simili a quelle usate per la simulazione relativa alla galassia, ho sviluppato una tabella che simula il viaggio dei fotoni della CMBR dalla loro partenza all’arrivo sulla Terra, prevedendo delle variazioni di velocità dei fotoni (dovuti al moto dei luoghi da loro via via percorsi) e del luogo della Terra, rispetto al luogo di partenza.

In breve risulta che nel periodo iniziale il luogo della Terra si allontana più velocemente e distanzia i fotoni, i quali in seguito, grazie alla decelerazione dell’espansione e, quindi, della velocità di allontanamento del luogo della Terra,  recuperano il ritardo e lo raggiungono.

Faccio osservare che alla fine del viaggio il luogo della Terra risulta lontano dal luogo di partenza della CMBR di circa 22 miliardi di anni luce (ultimo valore della colonna M). Valore che corrisponde al cosiddetto raggio dell’Universo osservabile.

Faccio anche rilevare che così come nella simulazione del viaggio dei fotoni della galassia, in base alla riduzione della velocità di allontanamento del luogo della Terra (F), risulta che l’espansione dell’Universo sia in decelerazione.

Per poter effettuare un confronto, ho provato a simulare il viaggio della CMBR anche in base al modello di Universo della CS, e ne è risultato un raggio di Universo estremamente più elevato di quello del modello di Universo qui presentato e, comunque, una velocità di espansione in fortissima decelerazione.
La differenza della lunghezza del raggio di Universo osservabile, tra i due modelli di Universo, è dovuta al fatto che nel presente modello viene usata la formula dell’effetto Doppler che vede la sorgente ferma e il ricevente in moto, mentre nel modello di Universo della CS, viene usata la formula che vede il ricevente fermo e la sorgente in moto, con la conseguenza che vengono ottenuti valori di espansione molto più elevati, anche se la CS considera il redshift come un fattore di espansione dello spazio (vedasi paragrafo 3.2).

Ho provato anche prevedere una velocità di espansione in accelerazione, ma non è risultato proprio possibile far arrivare la CMBR alla Terra, il che costituisce un punto molto importante a favore del modello di Universo qui presentato.

Vorrei fare un’ultima considerazione su questa simulazione.
Poiché, come ho scritto nel capitolo 2, lo scorrere del tempo varia in funzione della densità dello spazio e, quindi, verso il passato scorreva via via più velocemente, se ci fosse stato un orologio che avesse misurato il tempo sempre alla attuale velocità (potremmo immaginarlo come al di fuori dell’Universo), la vita dell’Universo sarebbe risultata inferiore ai 14 miliardi di anni. Naturalmente ho effettuato delle simulazioni ed è risultato che la sua vita sarebbe risultata di meno di 8 miliardi di anni.

3.5 Dimostrazione che il redshift non può essere il fattore di espansione dello spazio, così come considerato dalla Comunità Scientifica

In base alla tesi di laurea citata nel paragrafo 3.3, per la galassia oggetto della simulazione nel paragrafo 3.2, la luminosità apparente osservata risulta di circa il 25% minore rispetto a quella attesa, e cioè a quella risultante dall’applicazione della formula della CS. Il che  indicherebbe che la galassia si trova ad una distanza maggiore di quella prevista da modelli di Universo dominati da materia, per cui sarebbe determinata l’evidenza di un Universo in espansione accelerata.
In parole povere, ciò significherebbe che la distanza attuale osservata  della galassia, sarebbe maggiore di quella risultante dall’applicazione della formula della luminosità apparente, e cioè di quella attesa.
Per far comprendere meglio di cosa si tratta, espongo qui di seguito il calcolo della distanza attuale conoscendo quella iniziale ed il redshift.

Distanza attuale = Distanza iniziale x (1 + z)

Distanza attuale = 5,46 x (1 + 0,59) = 8,68

che corrisponde al valore esposto nell’articolo di Zappalà (2) come distanza attuale.

Ma se la distanza attuale osservata fosse veramente maggiore, significherebbe, naturalmente, che anche l'espansione dello spazio sarebbe stata maggiore di quella risultante utilizzando il fattore (1 + z).
Ma in questo caso anche il redshift dei fotoni, e quindi il fattore (1 + z) stesso, sarebbe stato maggiore di quello considerato, perché la maggiore espansione dello spazio si sarebbe riflessa anche sulla lunghezza d'onda dei fotoni e, quindi, sul fattore (1 + z).
E quindi la distanza attuale sarebbe risultata maggiore.
Ma dato che il fattore (1 + z) è quello osservato e non può aumentare, neanche la distanza attuale può aumentare.
Per cui se la distanza attuale risulta maggiore di quella attesa, può solo significare che il fattore (1 + z) non rappresenta l’espansione dello spazio avvenuta durante il viaggio dei fotoni.

Le stesse considerazioni valgono anche per la luminosità apparente, anche se il ragionamento da fare è un po’ più complesso. Eccolo.
Come sopra esposto, se la distanza attuale fosse veramente maggiore, significherebbe che l’espansione dello spazio sarebbe stata maggiore di quella risultante utilizzando il fattore (1 + z).
Ma in questo caso anche il redshift dei fotoni sarebbe stato maggiore e quindi il fattore (1 + z) stesso sarebbe stato maggiore.
Pertanto sarebbero risultati maggiori anche i valori dei fattori al denominatore della formula, corrispondenti sia alla distanza attuale (che, come sopra esposto, dipende dal fattore (1 + z)) che all’espansione dello spazio (1 + z), per cui sarebbe aumentato il valore totale del denominatore della formula, riducendo il suo risultato. 
E quindi la luminosità apparente attesa sarebbe risultata minore.
Ma dato che il fattore (1 + z) è quello osservato e non può aumentare, neanche la luminosità apparente può diminuire.
Per cui se la luminosità apparente osservata risulta minore di quella attesa, può solo significare che il fattore (1 + z) non rappresenta l’espansione dello spazio avvenuta durante il viaggio dei fotoni.

In conclusione le considerazioni sopra esposte dimostrano che il modello di Universo adottato, e cioè il fatto che l’Universo sia o non sia dominato dalla materia, non c’entra col fatto che la luminosità apparente osservata sia inferiore a quella attesa, perché dette considerazioni valgono per qualsiasi modello di Universo.
Per cui il ragionamento che il fatto che la luminosità apparente osservata sia inferiore a quella attesa, dimostrerebbe che non è stato adottato il giusto modello di Universo, non è valido. 
Pertanto non è valida neanche la conseguenza di detto ragionamento, e cioè che l’Universo risulti in espansione accelerata.

A sostegno della mia affermazione, riporto quanto ha scritto in merito il professor Alberto Franceschini dell’Università di Padova, in un suo corso di cosmologia (7), dove giustamente non ha motivato detta differenza con l’espansione dell’Universo in accelerazione: “Un risultato non comprensibile con la fisica che abbiamo sinora utilizzato nella nostra descrizione dell'Universo. Dobbiamo probabilmente fare ricorso ad una nuova fisica.”.

A mio parere, quindi, per giustificare la differenza tra la luminosità apparente attesa e quella osservata, è necessario trovare quale sia il fattore che rappresenti veramente l’espansione dello spazio avvenuta durante il viaggio, cosa che farò qui di seguito.

Come ho dimostrato tramite una simulazione tabellare del viaggio dei fotoni della galassia, esposta nel paragrafo 3.2, il redshift cosmologico è dovuto alla velocità di recessione del luogo dello spazio dove si trova la Terra alla ricezione dei fotoni, nei confronti del luogo dello spazio dove sono stati emessi i fotoni, e deve essere utilizzato come un fattore per calcolare una velocità e non come un fattore per calcolare un’espansione dello spazio.
Infatti in detta simulazione, che si basa su un modello di Universo diverso da quello considerato dalla CS, ho utilizzato i redshift cosmologici dei vari periodi del viaggio (coi quali ho calcolato le varie velocità di recessione), per calcolare la distanza attuale del luogo dello spazio dove si trova la Terra, dal luogo dello spazio dove si trovava l’oggetto celeste quando ha emesso i fotoni.
E poi, tenendo conto della riduzione di luminosità dovuta alla distanza effettivamente percorsa dai fotoni, ho utilizzato la luminosità apparente osservata per calcolare il fattore di espansione dello spazio avvenuta durante il viaggio, fattore che mi è servito per calcolare la distanza all’inizio del viaggio.
E, come si può vedere dai risultati della simulazione esposti in calce di questo paragrafo, è risultato che il valore del fattore di espansione dello spazio è maggiore del valore del redshift cosmologico.

Per calcolare tali velocità ho applicato la formula dell’effetto Doppler con l’emittente fermo e il ricevente in moto (come è realistico ipotizzare in base alla simulazione), e cioè (formula 3.2.2): 

velocità ricevente = c - c / (1 + z) ,  

per cui il valore 0,59 di z, corrisponde ad una velocità di allontanamento del ricevente rispetto all’emittente, di 111.321 km/s.

Mentre in base alla RR, per la quale ogni Sistema di Riferimento (SR) vede ogni altro SR in moto rispetto a se stesso (quindi con una visione tolemaica e pertanto irrealistica dell’Universo), si dovrebbe applicare la formula col ricevente fermo e l’emittente in moto, e cioè:

velocità emittente = z x c

per cui il valore 0,59 di z, corrisponderebbe ad una velocità di allontanamento dell’emittente rispetto al ricevente, di 177.000 km/s.
Però tale formula presenta un grosso problema, perché dalle osservazioni risulta che i fotoni provenienti dagli oggetti celesti molto lontani, hanno dei redshift con valori ben superiori a 1. Il che significherebbe che la loro velocità di allontanamento sarebbe ben superiore a quella della luce, cosa che sarebbe impossibile in quanto, in questo caso, la loro luce non sarebbe riuscita ad arrivare sulla Terra (questo problema non esiste se si applica la formula con l'emittente fermo ed il ricevente in moto, perchè la velocità del ricevente risulta sempre inferiore a quella della luce, qualsiasi sia il valore del redshift).

Pertanto volendo rispettare la RR, non si può considerare il redshift come dovuto alla velocità di allontanamento dell’emittente rispetto alla Terra.
Infatti la CS l’ha considerato come dovuto direttamente all’espansione dello spazio.
Ma così risulta che la luminosità apparente osservata è inferiore a quella attesa.

In conclusione il tutto dimostra che la RR non risulta compatibile con le osservazioni e che, quindi, risulta falsificata dal fatto che la luminosità apparente osservata delle supernove di tipo Ia, è inferiore a quella attesa.

Espongo qui di seguito i risultati significativi per il presente paragrafo relativi alla simulazione esposta nel paragrafo 3.2.

Distanza iniziale = 5,04 miliardi di anni luce;
Distanza attuale = 8,54 miliardi di anni luce;
F - distanza percorsa dai fotoni = 7 miliardi di anni luce;
z (redshift cosmologico dovuto a velocità recessione luogo della Terra) = 0,59;
Fattore di Espansione dello spazio = (8,54 – 5,04) : 5,04 = 0,69.
La velocità di espansione dello spazio, risulta in decelerazione.

4. CONCLUSIONI

Con questo articolo ho esposto alcune ipotesi compatibili con la teoria sul moto relativo allo spazio in espansione (1), che riassumo brevemente qui di seguito, su determinati fenomeni fisici.

4.1 Espansione dell’Universo

L’Universo è composto da un’infinità di piccolissime particelle di una uguale quantità di spazio (una sostanza che tende ad espandersi), che ho denominato come "quanti di spazio" e che tendono ad espandersi continuamente, causando l’espansione dell’Universo.

 
4.2 Gravità

La materia è formata da insiemi dinamici di quanti di spazio compressi e consente una maggiore espansione dei quanti vicini ad essa e poi via via di quelli più lontani.
Ogni oggetto materiale tende a muoversi verso i luoghi dove i quanti di spazio sono più espansi, e cioè verso altri oggetti materiali.

 
4.3 Velocità della luce variabile

La velocità della luce dipende dall’espansione dei quanti di spazio dei luoghi nei quali transita, ma poiché anche gli orologi si muovono in funzione di detta espansione, se misurate, sia la velocità che la frequenza della luce risultano sempre le stesse.
Pertanto, nel passato, quando l’espansione dello spazio era minore, la velocità della luce era maggiore.

4.4 Redshift cosmologico

Il redshift cosmologico è dovuto alla velocità di recessione del luogo dell’oggetto celeste che riceve il fotone, rispetto al luogo dell’oggetto celeste che l’ha emesso.
A sostegno di queste ipotesi ho presentato due tabelle che simulano il viaggio dei fotoni di una galassia ad alto redshift e quello dei fotoni della CMBR e, soprattutto, una formula che utilizza la luminosità apparente di un oggetto celeste ad alto redshift, per ricavare l'espansione dello spazio avvenuta durante il viaggio dei fotoni verso la Terra.
Il tutto fa risultare che la velocità di espansione dell’Universo sia in decelerazione, e non in accelerazione come sostenuto attualmente dalla CS, in base al suo modello di Universo.

In conclusione credo di aver dimostrato che il modello di Universo qui presentato, è almeno più compatibile con le osservazioni, di quello sostenuto dalla CS.

RIFERIMENTI

1. Dino Bruniera – Teoria sul moto relativo allo spazio in espansione;
2. Vincenzo Zappalà – C’è distanza e distanza - pubblicato in “astronomia.com”.
3. Matteo Billi - Vincoli cosmologici da supernovae ad alto redshift – Sommario – pagina V.
4. Annibale D'Ercole – L’accelerazione dell’universo.
5. Wikipedia, edizione italiana – Radiazione di fondo – Caratteristiche. ;
6. Amedeo Balbi – La musica del Big Bang – Capitolo 2, Paragrafo “Il lungo addio”. 2007 - 54-60;
7. A. Franceschini – Corso di cosmologia – Paragrafo 10.1.
8. Richard Feynman – SIX NOT-SO-EASY PIECES
https://nirstern.files.wordpress.com/2016/04/six-not-so-easy-pieces.pdf

Dino Bruniera

E-mail: dino.bruniera@gmail.com

HOME PAGE