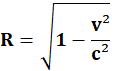
TEORIA SUL MOTO RELATIVO ALLO SPAZIO IN ESPANSIONE
RIASSUNTO
Col presente articolo mi propongo di dimostrare,
tramite la Radiazione di fondo, una teoria per la quale la luce si manifesta
nello spazio in espansione, per cui la sua velocità è isotropa solo nei suoi
confronti e non anche nei confronti degli oggetti celesti in moto rispetto ad
esso.
Pertanto il risultato dell’esperimento di Michelson e Morley, per il quale la
velocità della luce risulta isotropa in qualunque Sistema di Riferimento, è
dovuto al fenomeno ipotizzato da Lorentz, per il quale ogni oggetto subisce una
contrazione della sua lunghezza ed una dilatazione del suo tempo, in funzione
della sua velocità rispetto al mezzo nel quale si manifesta la luce, che in
questa teoria corrisponde allo spazio in espansione.
Quindi la Relatività Ristretta risulta sostituibile da una teoria per la quale
le onde luminose si manifestano nello spazio e la loro velocità non è isotropa
in tutti i Sistemi di Riferimento.
1. INTRODUZIONE
La teoria della Relatività Ristretta (RR) di Einstein è
una teoria “tolemaica”, e quindi non può essere compatibile con la realtà, in
quanto stabilisce che ogni Sistema di Riferimento (SR) consideri se stesso come
il centro dell’Universo e che la velocità della luce sia isotropa nei suoi
confronti.
Pertanto mi propongo di presentare una teoria della relatività più compatibile con la realtà, in quanto prevede che la velocità della luce
sia isotropa solo rispetto allo spazio in espansione e, quindi, non anche nei
confronti di qualsiasi oggetto celeste in moto nei suoi confronti.
2. DIMOSTRAZIONE CHE LA RELATIVITÀ RISTRETTA NON È COMPATIBILE CON LA REALTÀ
L'esperimento di Michelson e Morley (MM) del 1887,
avrebbe dovuto rilevare il cosiddetto vento d'etere, che sarebbe dovuto al moto
della Terra rispetto all'etere. E cioè al mezzo nel quale si manifesterebbe la
luce, e quindi il solo rispetto al quale la sua velocità sarebbe isotropa.
Per questa ragione l’etere sarebbe stato considerato come il SR Privilegiato.
Ma l'esperimento rilevò che la velocità della luce risultava isotropa e, quindi,
non rilevò alcun vento d'etere (1).
Per giustificare questo risultato negativo, Lorentz ipotizzò che tutti gli
oggetti che si muovono nell’etere, subiscano un rallentamento del tempo ed una
contrazione della lunghezza nella direzione del moto, in funzione della loro
velocità rispetto all’etere, facendo così risultare la velocità della luce come
isotropa, anche se in realtà non lo è (2).
Però nel 1905 intervenne Einstein, che non accettò la giustificazione di
Lorentz, "cancellò" la necessità dell'etere e formulò la teoria della RR, nella
quale ipotizzò che le onde luminose si propaghino nel vuoto e che la loro
velocità sia isotropa in tutti i SR.
Che sono ipotesi non realistiche, soprattutto perché le onde hanno bisogno di un
mezzo per manifestarsi, per cui la loro velocità può essere isotropa solo
rispetto a detto mezzo, come è la velocità del suono rispetto all’aria.
Lo stesso Einstein, nel 1920, modificò le sue convinzioni su questa ipotesi,
scrivendo che si può accettare “l’introduzione di un mezzo che riempie lo spazio
ed assumere che i campi elettromagnetici siano i suoi stati” (3), ma
senza giustificare come sia possibile che quel mezzo non sia considerato come il
SR privilegiato, e cioè il solo rispetto al quale la velocità della luce sia
realmente isotropa.
Comunque Einstein affermò che l’isotropia della velocità della luce in ogni SR,
“non è nella realtà né una supposizione né un’ipotesi circa la natura fisica
della luce, bensì una convenzione che io posso fare a mio arbitrio al fine di
giungere a una definizione di simultaneità” (4).
Quindi Einstein ipotizzò che la velocità della luce sia isotropa in tutti
i SR, non perché effettivamente possa esserlo, ma per una convenzione.
Nonostante questa precisazione di Einstein, la RR è stata accettata come
conforme alla realtà dalla CS, probabilmente soprattutto per la sua
compatibilità con la Relatività Generale (RG), la quale ha fornito una legge
sulla gravità più aderente con le osservazioni rispetto a quella fornita da
Newton.
Però questa ipotesi comporta una visione piuttosto “tolemaica” dell’Universo, e
quindi non realistica, in quanto ogni SR considera se stesso fermo e tutti gli
altri SR in moto rispetto a se stesso e, quindi, si considera come al centro
dell’Universo.
Il che comporta, tra l’altro, che il redshift cosmologico non sia compatibile con
la RR (5).
3. MOTO RELATIVO ALLO SPAZIO IN ESPANSIONE
3.1 Esposizione
Una visione più realistica è quella che prevede che la
velocità della luce sia isotropa solo nei confronti del mezzo nel quale
essa si manifesta, che consiste nell’unica sostanza che compone l’Universo e che
corrisponde a ciò che viene denominato come spazio.
In questo articolo ho denominato il mezzo nel quale si manifesta la luce, come
“spazio”, ma avrei potuto denominarlo anche come “etere” o, ancora meglio, come
“apeiron”, che è il termine col quale, circa 26 secoli fa, il filosofo greco
Anassimandro ha denominato la sostanza primordiale.
Anche due fisici importanti, quali Werner Heisenberg e Max Born, hanno
ipotizzato che l’Universo sia composto da un’unica sostanza nella quale si
manifesterebbe sia la luce che qualunque altra particella elementare, come
risulta da quanto esposto su Wikipedia:
“Werner Heisenberg, noto per la creazione della meccanica quantistica, è
arrivato a pensare che le particelle elementari sono da considerare come
differenti manifestazioni, differenti stati quantici, di una stessa “sostanza
primordiale”. Per la similarità con la sostanza primordiale ipotizzata da
Anassimandro, il suo collega Max Born ha denominato questa sostanza come
“apeiron””.
La teoria che presento non si basa sulla sopra citata
irrealistica convenzione “tolemaica” della RR, ma su una convenzione realistica,
per la quale il luogo dello spazio in espansione nel quale sta transitando un
oggetto celeste, viene considerato come il suo SR privilegiato, e cioè quello
nel quale la velocità della luce che sta transitando vicino all’oggetto, è
veramente isotropa.
Detta teoria è compatibile con la Teoria dell’etere di Lorentz (TEL) e, quindi,
anche con le sue giustificazioni sui risultati dei vari esperimenti sulla
velocità della luce, compreso quello di MM.
Inoltre da essa si possono derivare delle ipotesi sui vari fenomeni
dell'Universo, quali la sua espansione, la gravità, la velocità della luce, il
redshift cosmologico, la luminosità apparente degli oggetti celesti ad alto
redshift, più aderenti con le osservazioni rispetto a quelle attualmente
sostenute dalla Comunità Scientifica (6).
3.2 Identificazione del SR privilegiato
Dalle osservazioni risulta che lo spazio, che considero
come una “sostanza” nella quale si manifestano sia i fotoni che la materia, si
sta espandendo in tutto l’Universo.
In base alla teoria del Big Bang, circa 379.000 anni dopo l’inizio della sua
espansione, lo spazio è diventato trasparente alla radiazione, per cui
un’enorme quantità di fotoni ha iniziato a propagarsi liberamente (7, 8).
Per cui essi, a differenza degli altri fotoni, che vengono emessi da oggetti
celesti in moto rispetto allo spazio, è come se fossero stati emessi dallo
spazio stesso. Pertanto, poiché la frequenza dei fotoni è isotropa solo nei
confronti dell'emittente, sono gli unici fotoni la cui frequenza risulta
pressoché isotropa nei confronti dello spazio.
I fotoni sono partiti da luoghi diversi dello spazio ed hanno viaggiato in
direzioni casuali, per cui una parte di essi ha viaggiato in direzione della
Terra.
Da allora tali fotoni, che vengono denominati come radiazione cosmica di fondo
(abbreviata in CMBR, dall'inglese Cosmic Microwave Background Radiation), hanno
continuato ad arrivare sulla Terra, a cominciare da quelli partiti dai luoghi
più vicini e poi via via, da quelli sempre più lontani.
A causa dell'espansione dello spazio, la loro lunghezza d’onda è notevolmente
aumentata, e quindi la loro frequenza è diminuita, fino al valore attualmente
rilevato di circa 1.100 volte, che è lo stesso per tutti i fotoni, salvo alcune
lievissime anisotropie dell'ordine di una parte su 100.000 (7).
Oltre a dette anisotropie, che sono di natura intrinseca alla CMBR, è stata
rilevata una particolare anisotropia di ben maggiore ampiezza rispetto alle
altre (di circa una parte su 1.000), che dipende dalla direzione di provenienza
della CMBR e che risulta dovuta al moto della Terra (di circa 370 km/s) rispetto
ad un determinato luogo nel quale detta anisotropia non verrebbe rilevata, e che
viene denominata “anisotropia di dipolo” (9).
Per cui in tale luogo risulterebbe che la frequenza della CMBR sarebbe isotropa
(senza tener conto delle sopra citate lievissime anisotropie) o, più
precisamente, che non sarebbe influenzata dall'anisotropia di dipolo. Come è
prevedibile dal fatto che detti fotoni è come se fossero emessi dallo spazio
stesso, come ho dimostrato sopra. Ma anche la sua velocità è isotropa, perché
tale luogo fa parte dello spazio e, quindi, del mezzo tramite il quale i fotoni
si manifestano.
Quindi in detto luogo sia la velocità che la frequenza della CMBR (senza tener
conto delle sopra citate lievisime anisotropie), risulterebbero isotrope, com’è
corretto che debba essere e come verrà dimostrato anche nel prossimo paragrafo.
Detto luogo non può che essere
quello dove la frequenza della CMBR viene misurata, e cioè quello dove la Terra
sta transitando nel momento della misura.
La velocità dei fotoni non può essere isotropa neanche rispetto a luoghi
diversi da quello che i fotoni stanno percorrendo, perché a causa
dell’espansione dello spazio, gli altri luoghi si stanno allontanando da detto
luogo e, quindi, risultano in moto rispetto ad esso (questo ragionamento verrà
approfondito nel prossimo paragrafo).
Pertanto, per quanto riguarda la Terra, la velocità dei fotoni è isotropa solo
nei confronti del luogo dello spazio dove la Terra sta transitando e non anche
nei confronti della Terra. Quindi tale luogo costituisce il suo SR privilegiato.
La velocità con la quale la Terra si sta muovendo rispetto al suo SR
privilegiato, viene determinata dal valore dell’anisotropia di dipolo.
Naturalmente ogni oggetto celeste avrà il suo SR privilegiato, che corrisponde
al luogo dello spazio nel quale esso sta transitando.
3.3 Esposizione del modello di Universo tramite esempi mentali
Si immagini lo spazio in espansione come una grande
sfera di gomma che si stia gonfiando continuamente e sulla cui superficie siano
segnati moltissimi punti (raffigurano i luoghi dello spazio).
Si immaginino poi i fotoni della CMBR come degli insiemi di automobiline che si
muovano sulla sua superficie a velocità costante, poniamo di 1 m/s.
Si noti che se la velocità di un’automobilina è di 1 m/s rispetto al punto in
cui sta transitando, non può essere di 1 m/s anche nei confronti degli altri
punti, in quanto essi, a causa dell’espansione della superficie della sfera, si
stanno allontanando da tale punto. Quindi per determinare la sua velocità
rispetto ad uno degli altri punti, bisognerà addizionare o sottrarre da 1 m/s,
la velocità di allontanamento del punto interessato, in funzione della direzione
del moto dell’automobilina rispetto a tale punto. Di conseguenza, rispetto a
tale punto, le automobiline che vanno in direzione contraria a quella del punto, hanno una velocità
superiore ad 1 m/s, e quelle che
vanno nella stessa direzione del punto, hanno una velocità inferiore ad 1 m/s.
Quindi la velocità delle automobiline che transitano in un determinato punto,
non è isotropa rispetto ad un altro punto. Per il quale, naturalmente, è
isotropa la velocità delle automobiline che transitano in esso.
Si immagini poi un SR come un camioncino che si muova sulla superficie della
sfera, ma ad una velocità inferiore ad 1 m/s, e poniamo che riesca a misurare la
sua velocità nei confronti delle automobiline. Allora rileverebbe che esse gli
si avvicinano a velocità diverse a seconda della direzione, e con adeguati
calcoli potrebbe determinare la sua velocità rispetto al punto che sta
percorrendo.
Per esempio se misurasse la velocità di due sole automobiline provenienti da
direzioni opposte e questa fosse rispettivamente di 0,9 e 1,1 m/s, la differenza
sarebbe di 0,2 m/s e la sua velocità rispetto a tale punto, risulterebbe della
metà, e cioè di 0,1 m/s.
Ma se il camioncino rilevasse la velocità di 1 m/s per tutte e due le
automobiline (il che raffigurerebbe l'esperimento di MM), significherebbe che
non ha gli strumenti adeguati per rilevare l’esatta velocità e non che le
automobiline gli vengano incontro realmente a 1 m/s, in quanto ciò sarebbe
impossibile.
Poniamo che in uno dei punti segnati sulla sfera, transitino due colonne di
automobiline, provenienti da direzioni opposte e distanziate di 0,1 metri l’una
dall’altra.
Un osservatore posizionato in tale punto, in un secondo conterebbe 10
automobiline provenire da una direzione e 10 dall’altra, e misurerebbe una
velocità di 1 m/s per ciascuna di esse.
Pertanto sia la frequenza di automobiline che la loro velocità, gli
risulterebbero isotrope.
Ora ponendo che il camioncino si muova sempre alla velocità di 0,1 m/s verso una
delle due direzioni, in un secondo conterebbe 11 automobiline provenire dalla
direzione verso la quale si sta muovendo e 9 automobiline dalla direzione
contraria. Quindi rileverebbe una differenza di 2 automobiline tra le due
direzioni di provenienza (la differenza raffigura l'anisotropia di dipolo della
CMBR). E se misurasse correttamente la velocità delle automobiline rispetto a sé
stesso, troverebbe che quelle provenienti dalla direzione frontale, avrebbero
una velocità di 1,1 m/s, mentre quelle provenienti da dietro, avrebbero una
velocità di 0,9 m/s.
Pertanto sia la frequenza che la velocità delle automobiline, dipenderebbero
dalla direzione di provenienza e, quindi, gli risulterebbero anisotrope.
Ma se misurasse la loro velocità isotropa (1 m/s) e la frequenza anisotropa (11
e 9), significherebbe che una delle due misure non sarebbe corretta, e cioè
quella della velocità, come risulta dall’esempio precedente.
In conclusione risulta che la velocità delle automobiline è realmente isotropa
solo nei confronti del punto che stanno percorrendo, il quale, pertanto,
costituisce il SR privilegiato per il camioncino.
Per completezza vorrei aggiungere che, naturalmente, ogni punto nel quale il
camioncino transiterà durante il suo viaggio, nel momento del transito
costituirà il suo SR privilegiato, ma non lo sarà più una volta superato.
4. SVILUPPI
4.1 Tempo e lunghezza
Dalle dimostrazioni sopra esposte si possono dedurre le leggi fisiche che seguono.
Ogni luogo dello spazio ha un proprio tempo, che qui
denomino come tempo locale.
In un eventuale oggetto che transitasse in detto luogo, il tempo
corrisponderebbe al tempo locale dilatato in funzione della sua velocità
rispetto al luogo stesso, e si ottiene applicando la formula di Lorentz sulla
dilatazione del tempo (le formule sono esposte nel prossimo paragrafo).
Di conseguenza conoscendo il tempo nell’oggetto, è possibile ottenere il tempo
locale, applicando la formula di Lorentz inversa sulla dilatazione del tempo.
Un ipotetico oggetto a riposo rispetto ad un luogo dello
spazio, assumerebbe la lunghezza massima, che qui denomino come lunghezza
locale.
Un oggetto che transitasse in detto luogo, subirebbe una contrazione della sua
lunghezza nella direzione del suo moto, in funzione della sua velocità rispetto
al luogo stesso. La lunghezza contratta si ottiene applicando la formula di
Lorentz sulla contrazione delle lunghezze.
Di conseguenza conoscendo la lunghezza contratta, è possibile ottenere la
lunghezza locale, applicando la formula di Lorentz inversa sulla contrazione
delle lunghezze.
Lo strumento per misurare la velocità dell’oggetto rispetto al luogo dove esso sta transitando, è costituito dalla anisotropia di dipolo della CMBR.
4.2 Formule di Lorentz
In pratica si tratta di due semplici formule matematiche, con le relative formule inverse, con le quali Lorentz ha giustificato il risultato negativo dell’esperimento di MM.
Definizioni
Definisco come S0 un ipotetico SR privilegiato, cioè un determinato luogo dello spazio.
Definisco come S1
un SR in moto rispetto a S0.
t = tempo
l = lunghezza
c = velocità della luce
v = velocità rispetto a S0
Fattore di contrazione e/o dilatazione
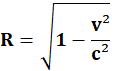
Dilatazione del tempo: calcolo del tempo di un orologio posto in S1, conoscendo quello di un orologio posto in un S0 (tempo locale).
![]()
Dilatazione del tempo, inversa: calcolo del tempo di un orologio posto in S0
(tempo locale), conoscendo quello di un orologio posto in S1.
![]()
Contrazione delle lunghezze: calcolo della lunghezza di un oggetto posto in
S1, conoscendo quella dell’oggetto posto
in S0.
![]()
Però se misurato in S1 l’oggetto risulterà comunque della stessa lunghezza, perché anche il regolo per misurarlo si contrae.
Contrazione delle lunghezze, inversa: calcolo della lunghezza di un oggetto posto in S0, conoscendo quella dell’oggetto posto in S1.
![]()
4.3 Differenze con la Relatività Ristretta
Nei confronti della RR ci sono le differenze che seguono.
Per la presente teoria la velocità dei fotoni è isotropa
solo rispetto alla località che stanno percorrendo.
Per la RR essa è isotropa anche rispetto agli oggetti che vi stanno transitando.
Per la presente teoria ogni oggetto assume una
conformazione in funzione della sua velocità nei confronti del luogo dello
spazio nel quale sta transitando, nel senso che la sua lunghezza si contrae ed
il suo tempo si dilata.
Per la RR ogni oggetto osserva gli altri oggetti che si contraggono ed il loro
tempo che si dilata, in funzione della loro velocità rispetto a se stesso.
5. CONCLUSIONI
La velocità della luce rispetto alla Terra, non può
essere isotropa per i motivi che seguono.
1. Da quanto risulta dalle spiegazioni tramite esempi mentali (paragrafo 3.3), affinché la
velocità dei fotoni della CMBR, possa essere veramente isotropa, è necessario
che anche la loro frequenza ondulatoria risulti isotropa, quindi dato che sulla
Terra tale frequenza non risulta isotropa, ma dipende dalla direzione di
provenienza, significa che neanche la loro velocità possa essere isotropa, ma
che dipenda dalla direzione di provenienza.
2. Da quanto risulta dal paragrafo sulla identificazione del SR privilegiato
(3.2),
nel luogo dello spazio percorso dalla Terra, sia la velocità che la frequenza
dei fotoni della CMBR, sono isotrope. Il che significa che la loro velocità è realmente
isotropa, per cui non può essere realmente isotropa anche rispetto alla Terra,
dato che essa vi transita alla velocità di circa 370 km/s.
Naturalmente se la velocità dei fotoni della CMBR non è isotropa, neanche la
velocità degli altri fotoni può essere isotropa.
Quindi se nella Terra la velocità dei fotoni risulta ugualmente isotropa, come
nell’esperimento di MM, significa solo che nella Terra gli strumenti non sono in
grado di misurarla correttamente e non che essa sia realmente isotropa.
Pertanto la velocità dei fotoni è isotropa solo rispetto ai luoghi dello spazio
da essi via via percorsi, che quindi possono essere definiti come i SR
privilegiati per gli eventuali oggetti che vi transitassero.
Da queste dimostrazioni si ricava una teoria per la quale
per ogni oggetto ed in ogni momento, esiste un SR privilegiato, che consiste nel
luogo dello spazio dove esso sta transitando, rispetto al quale:
- la velocità dei fotoni è realmente isotropa;
- l’oggetto può misurare la sua velocità;
- l’oggetto si contrae in funzione della sua velocità;
- il tempo nell’oggetto si dilata in funzione della sua velocità.
Lo strumento per misurare detta velocità, è l’anisotropia di dipolo della CMBR.
RIFERIMENTI
1. Max Born – “La sintesi einsteiniana” – Capitolo
5, paragrafo 14 - “L’esperimento di Michelson e Morley”. 1973 - 257-262;
2. Max Born – “La sintesi einsteiniana” – Capitolo 5, paragrafo 15 –
“L’ipotesi della contrazione”. 1973 - 262-269;
3. Albert Einstein – Morgan manuscript – paragrafo 13 – 1920;
4. Albert Einstein – Relatività: Esposizione divulgativa – Capitolo 1,
paragrafo 8 – “Sul concetto di tempo nella fisica”. 1996; 58-61;
5. Dino Bruniera – “Relativita-ristretta-incompatibile-con-redshift-cosmologico”;
6. Dino Bruniera - “Ipotesi basate sulla teoria sul moto relativo allo
spazio in espansione”;
7. Wikipedia, edizione italiana – Radiazione di fondo – Caratteristiche;
8. Amedeo Balbi – La musica del Big Bang – Capitolo 2, Paragrafo “Il lungo
addio”. 2007; 54-60;
9. Amedeo Balbi – La musica del Big Bang – Chapter 3, Paragrafo “I
giganti del cosmo”. 2007, 80-85.
Dino Bruniera
E-mail: dino.bruniera@gmail.com